Week 4

Initial conditions and temperature

Eventually we would like to study the behaviour of the Argon atoms under different environmental conditions and even study the different thermodynamic phases. To do so, we will have to enforce the appropriate parameters, such as temperature and density. This can be achieved by initializing the atoms in a suitable configuration. In particular, we need to carefully set up the initial positions and velocities with these goals in mind.

Positions

The choice for the initial conditions for the position is influenced by two aspects:

1. We do not want the particles to start too close to each other, otherwise the $r^{-12}$ repulsive potential will give a very large energy. Hence, putting particles on some sort of regular grid with a set spacing is sensible.

2. Eventually we will want to simulate phase transitions, for example from solid to liquid. Given the fact that Argon forms a face centred cubic (fcc) lattice in its solid state, we should therefore choose a number of particles $N$ that is compatible with an fcc lattice.

These two aspects are most easily satisfied by choosing the initial positions to be on an fcc lattice. This is also what we recommend you to do! As a reminder, the fcc unit cell is such that one atom is placed at each of the 8 corners of the cube, and also at the center of each of the 6 faces, for a total of 14 particles per unit cell. Furthermore, it can be encoded by a simple set of primitive vectors.

Velocities and temperature

As many of you might have already done, the initial velocities should be chosen such that they obey a Maxwell-Boltzmann distribution for temperature $T$. This is obtained by chosing the $v_x$, $v_y$, and $v_z$ coordinates according to a Gaussian distribution

$$e^{-m v_{x,y,z}^2/(2 k_B T)}$$

Don't forget to properly normalize it! We also suggest to subtract the velocity of the center of mass, so that the average velocity is 0 in all directions. This keeps the collective of all atoms from drifting.

Given the above, one might think that we can simply set the temperature of our system in a single step by generating the velocity distribution. But, in fact, this is not the case: when the simulation fist starts evolving it will equilibrate, and energy will be exchanged between kinetic and potential energy terms. It is hard to predict how exactly this will happen, and therefore the solution is to instead let the system equilibrate for a while and then again force the kinetic energy to have a value corresponding to a certain temperature.

This can be done by rescaling the velocities:

$$\mathbf{v}_i \rightarrow \lambda \mathbf{v}_i$$

with the same parameter $\lambda$ for all particles. From the equipartition theorem we know that

$$E_\text{kin} = (N-1) \frac{3}{2} k_B T$$

where there is the small subtlety that we have $N-1$ instead of $N$. The reason for this is that in the equipartion theorem we count the number of independent degrees of freedom, which one would naively assume to be $N$. However, the total velocity in our system is conserved:

$$\frac{d}{dt} \sum_i \mathbf{v}_i = \sum_{i\neq j} \frac{1}{m} \mathbf{F}_{ij} = 0$$

as the sum over all forces from the pair interaction must vanish. The velocity of the last particle is therefore fixed by that of all other particles.

Combining the above, the equipartition theorem results in the following rescaling factor $\lambda$:

$$\lambda = \sqrt{\frac{(N-1) 3 k_B T}{\sum_i m v_i^2}}$$

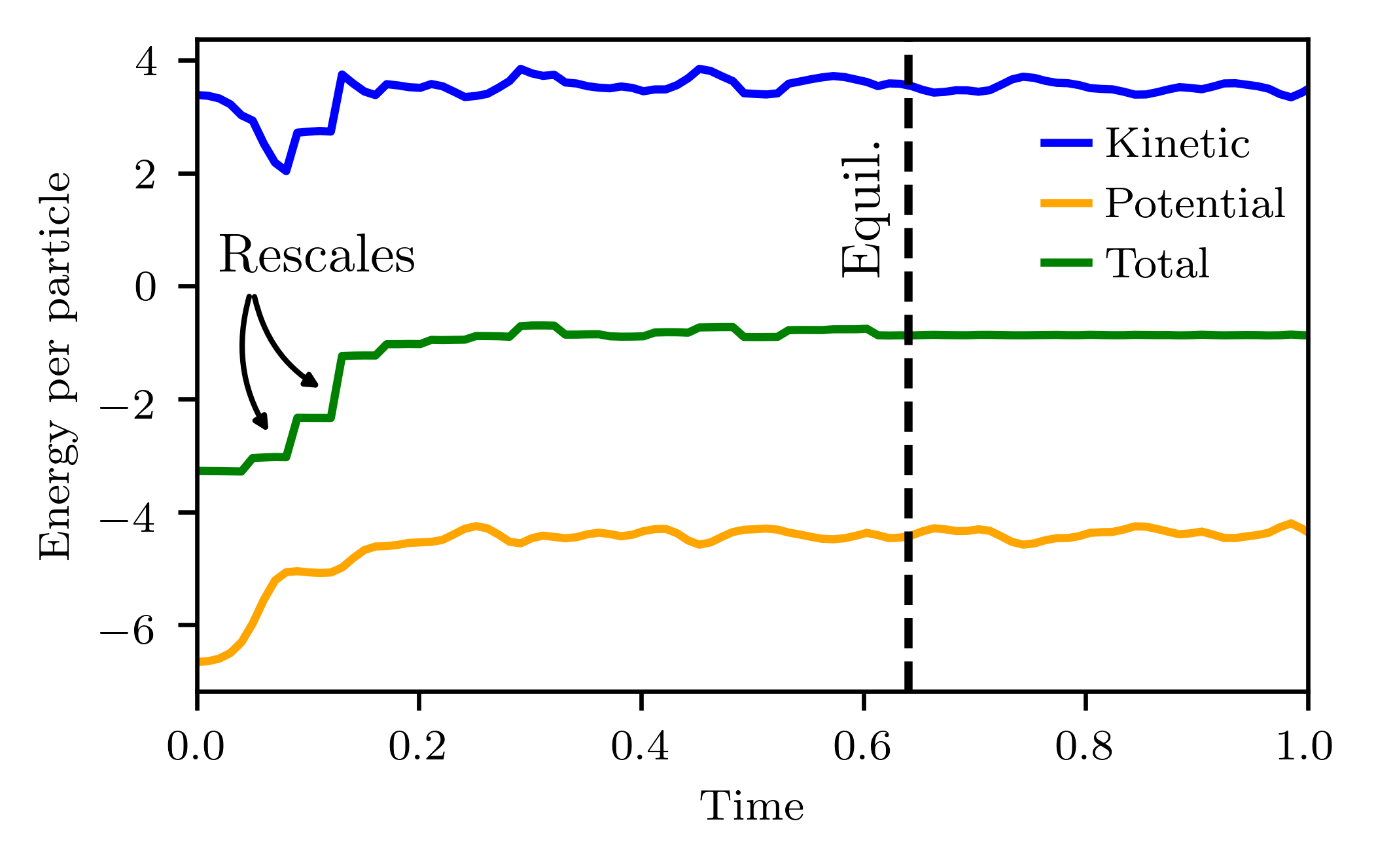
In order to get the system to settle on the desired temperature $T$ one thus needs to apply an iterative method. After initializing the velocities the system is allowed to equilibrate for a certain amount of time, after which the rescaling with $\lambda$ is performed. This rescaling is then again followed by a new period of equilibration, after which it is checked if the desired temperature has been reached. If this has not yet occured, the procedure is repeated, until the temperature finally does converge. Note that this procedure is essentially part of the initialization of the system. Any physical quantity that one would like to observe should be measured after the desired temperature is reached! This procedure is illustrated below:

Note: The formulas above are not in dimensionless units yet! To use it in a simulation with dimensionless units you need to convert them. This is a good exercise, if you have problems with it feel free to ask!

Observables

After having implemented all of the above steps, you now have a program that simulates the microscopic behavior of Argon atoms. Our goal is now to quantify their behavior by computing macroscopic observables, which can then be compared to theory and literature.

To this end we have to perform statistical averages, denoted as $\langle ... \rangle$. In statistical mechanics, this would correspond to an average over all the possible realizations in an ensemble. In our molecular dynamics simulation, this is replaced by an average over simulation time:

$$\langle A\rangle = \frac{1}{n-n_0} \sum_{\nu>n_0}^{n}{A_\nu}$$

where the indices $\nu$ label the timesteps of the numerical integration, taking account only those occuring after the $n_0$ time steps used to equilibrate and converge to the desired temperature.

In what follows we give a minimal description of the quantities and formula's involved; we refer to the book "Computational Physics" (specifically chapter 8) and the references therein for details.

Pair correlation function

A good measure for the presence or absence of structure in a large collection of moving particles is the pair correlation function, also known as the radial distribution function. Simply put, it is a measure of the probability of finding a particle at a distance of $r$ away from a given reference particle, relative to an ideal gas. This distribution has very specific forms in the different states of matter, and it can thus be used to identify the different thermodynamic states.

In the simulation, you can compute the pair correlation by making a histogram $n(r)$ of all particle pairs within a distance $[r, r+\Delta r]$, where $\Delta r$ is the bin size. The pair correlation function is then given by

$$g(r) = \frac{2V}{N(N-1)} \frac{\langle n(r) \rangle}{4 \pi r^2 \Delta r}$$

where $V$ is the volume of the simulation cell, and $N$ the number of particles. The constants ensure normalization with respect to the ideal gas, where particle histograms are uncorrelated. Be sure to compute the distances of every particle to every other particle. So not only one particle's distances to every other particle.

Pressure

Next we want to calculate two well-behaved and well-known macroscpic observables: pressure and specific heat.

Starting with pressure, it might not immediately be obvious how to calculate such a macroscopic quantity based on the microscopic parameters we have available to us in a molecular dynamics simulation. However, this can be done using the virial theorem (for a derivation see 1):

$$\frac{\beta P}{\rho} = 1 - \frac{\beta}{3 N} \left<\frac{1}{2} \sum_{i,j} r_{ij} \frac{\partial U}{\partial r_{ij}} \right>$$ where $\beta=1/k_B T$, $\rho$ is the density, $N$ is the number of particles, and $r_{ij}$ is the distances between a pair of particles.

Note: The above expression makes use of the virial, which is typically written as $\left<\sum_i \mathbf{r}_i \mathbf{F}_i\right>$. While this expression is correct in the infinite system limit, it has troubles with periodic boundary conditions. This problem is solved in the expression given above.

Specific heat

Another observable of interest is the specific heat $C_V$. In the canonical ensemble this is readily evaluated from fluctuations in the total energy, but in the microcanonical ensemble the total energy is fixed and these fluctuations vanish. However, as derived by Lebowitz it can be calculated from fluctuations in the kinetic energy instead: $$\frac{\langle \delta K^2 \rangle}{\langle K \rangle^2} = \frac{2}{3N} \left(1-\frac{3N}{2 C_V}\right) = \frac{2}{3N} \left(1-\frac{3}{2 c_V}\right)$$ where $K$ is the kinetic energy, and $\langle\delta K^2\rangle= \langle K^2 \rangle - \langle K \rangle^2$ the fluctuations of the kinetic energy. In this formula $C_V$ is the total specific heat capacity for all $N$ atoms, whereas $c_V=C_V/N$ is the specific heat per atom.

Diffusion

Another useful quantity to investigate is how individual atoms move around over time. This can be done using the mean-squared displacement (MSD):

$$\langle \Delta^2\textbf{x}(t)\rangle = \langle \left[ \textbf{x}(t)-\textbf{x}(0) \right] ^2\rangle$$ where $\textbf{x}(0)$ is a suitably chosen starting point.

This quantity essentially encodes the relationship between the particle positions and velocities at the initial time $t=0$ and their positions at time $t$. That relathionship can be very simple, for example in the case of an ideal gas where there are no interactions and particles simply move along straight lines. In this case $\textbf{x}(t) = \textbf{x}(0)+\textbf{v}(0)t$ and the MSD is given by $$\langle \Delta^2\textbf{x}(t)\rangle = \langle \textbf{v}(0)^2\rangle t^2 = 3v_0^2 t^2$$

where $v_0^2 = k_B T/m$ is the mean-squared velocity of the Maxwell-Boltzmann distribution. This simple results says that in a gas without collisions (also known as the ballistic case) the mean squared displacement will grow quadratically with time.

Since any collision will have the effect of slowing down the particles, one can expect that when interactions become relevant the MSD will not grow as quickly. Indeed, in the case of a liquid one can show that for timescales long compared to the typical interaction time the MSD instead grows linearly. This linear dependence is in fact the defining characteristic of diffusive motion. In the linear regime, one can estimate the diffusion coefficient to the slope of the MSD through the Einstein relation:

$$D = \lim_{t\rightarrow \infty} \frac{1}{6t} \langle \Delta^2\textbf{x}(t)\rangle$$

Finally, there is the case of a solid. In a solid state the MSD will eventually reach a plateau related to the characteristic vibrational frequency, where the slope and therefore $D$ is effectively zero. In reality there is still some diffusion in the solid, although it will be several orders of magnitude smaller than in a liquid.

Note: At short times $\langle \Delta^2\textbf{x}(t)\rangle$ will increase like $t^2$ for all three systems (gas, liquid, solid). This can be seen by making a Taylor series of $\textbf{x}(t)$ and evaluating the MSD; one simply obtains the case of the ideal gas plus higher order corrections. It is therefore essential to let the system evolve for timescales that are long compared to typical interactions if you want to observe these different types of behaviour.

Milestones

• Implement the initialization of positions onto an fcc lattice.
• Show that the initial velocities obey a Maxwell-Boltzmann distribution.
• Perform the rescaling of temperature and show how the desired temperature is attained after a certain amount of rescaling and equilibrating.
• Study at least one observable, and compare its behaviour to literature.