Week 3

Better time propagation

The normal Euler methods for integrating ordinary differential equations (ODEs) have a major downside for the molecular dynamics simulations we are doing: they do not conserve the total energy of the system very well. This is a problem, as our goal is to simulate a system with conserved energy (the microcanonical ensemble). We'll therefore derive and move on to a better algorithm.

The Verlet algorithm

The algorithm we will focus on was introduced at the very beginning of the field of molecular dynamics (see the classic paper of Verlet from 1967). It directly makes use of the fact that we have a second order ODE:

$$\frac{d^2 \mathbf{x}}{dt^2}= \mathbf{F}(\mathbf{x}(t))$$

Note: in the above we are we working in dimensionless units and in addition we do not explicitly write $\mathbf{x} = \{x_0, x_1, \dots, x_N\}$.

For this equation we can easily derive a finite time-step algorithm by using the Taylor expansion of $\mathbf{x}(t\pm h)$:

$$\begin{aligned} \mathbf{x}(t+h) = & \mathbf{x}(t) + h \dot{\mathbf{x}}(t) + \frac{h^2}{2} \ddot{\mathbf{x}}(t) + \frac{h^3}{6} \frac{d^3}{dt^3}\mathbf{x}(t) + \mathcal{O}(h^4)\\ \mathbf{x}(t-h) = & \mathbf{x}(t) - h \dot{\mathbf{x}}(t) + \frac{h^2}{2} \ddot{\mathbf{x}}(t) - \frac{h^3}{6} \frac{d^3}{dt^3}\mathbf{x}(t) + \mathcal{O}(h^4) \end{aligned}$$

Adding those two equations together and using $\ddot{\mathbf{x}}=\mathbf{F}$, we find

$$\mathbf{x}(t+h) = 2 \mathbf{x}(t) - \mathbf{x}(t-h) + h^2 \mathbf{F}(\mathbf{x}(t))$$

However, in the first time-step we have no information about $\mathbf{x}(t-h)$. We therefore need to replace it by $\mathbf{x}(t-h) = \mathbf{x}(t) - h \mathbf{v}(t) +\mathcal{O}(h^2)$.

In this version of the Verlet algorithm, only the positions enter. Velocities (that we need for the kinetic energy!) have to be estimated from

$$\mathbf{v}(t) = \frac{\mathbf{x}(t+h) - \mathbf{x}(t-h)}{2h} + \mathcal{O}(h^2)$$

Velocity-Verlet

The algorithm can be slightly modified to directly use velocities. For that we take the Taylor expansion of $\mathbf{x}(t+h)$ and replace $\dot{\mathbf{x}} = \mathbf{v}$ and $\ddot{\mathbf{x}}=\mathbf{F}$ to arrive at

$$\mathbf{x}(t+h) = \mathbf{x}(t) + h \mathbf{v}(t) + \frac{h^2}{2} \mathbf{F}(\mathbf{x}(t))$$

Additionally, we need now an equation for $\mathbf{v}$. We do a Taylor expansion for $\mathbf{v}$ (you see, in the end it's always Taylor expansion!)

$$\mathbf{v}(t+h) = \mathbf{v}(t) + h \dot{\mathbf{v}}(t) + \frac{h^2}{2} \ddot{\mathbf{v}}(t) + \mathcal{O}(h^3)$$

We know that $\dot{\mathbf{v}} = \mathbf{F}$ but we don't know $\ddot{\mathbf{v}}$. So for this we Taylor expand (again!!)

$$\dot{\mathbf{v}}(t+h) = \dot{\mathbf{v}}(t) + h \ddot{\mathbf{v}}(t) + \mathcal{O}(h^2)$$

from which we find $\ddot{\mathbf{v}}(t) = \frac{1}{h} (\mathbf{F}(\mathbf{x}(t+h)) - \mathbf{F}(\mathbf{x}(t))$. Inserting this back we finally find the velocit-Verlet algorithm:

$$\begin{aligned} \mathbf{x}(t+h) = & \mathbf{x}(t) + h \mathbf{v}(t) + \frac{h^2}{2} \mathbf{F}(\mathbf{x}(t))\\ \mathbf{v}(t+h) = & \mathbf{v}(t) + \frac{h}{2} \left(\mathbf{F}(\mathbf{x}(t+h)) + \mathbf{F}(\mathbf{x}(t))\right) \end{aligned}$$

Case study: the 2 body gravitational problem

We illustrate the difference between the two integration methods studying the simple case of a (3D) 2-body gravitational problem. Specifically, that of the earth and the sun. In this case, it turns out that using Euler's method generally results in the earth slowly spiralling into the sun: 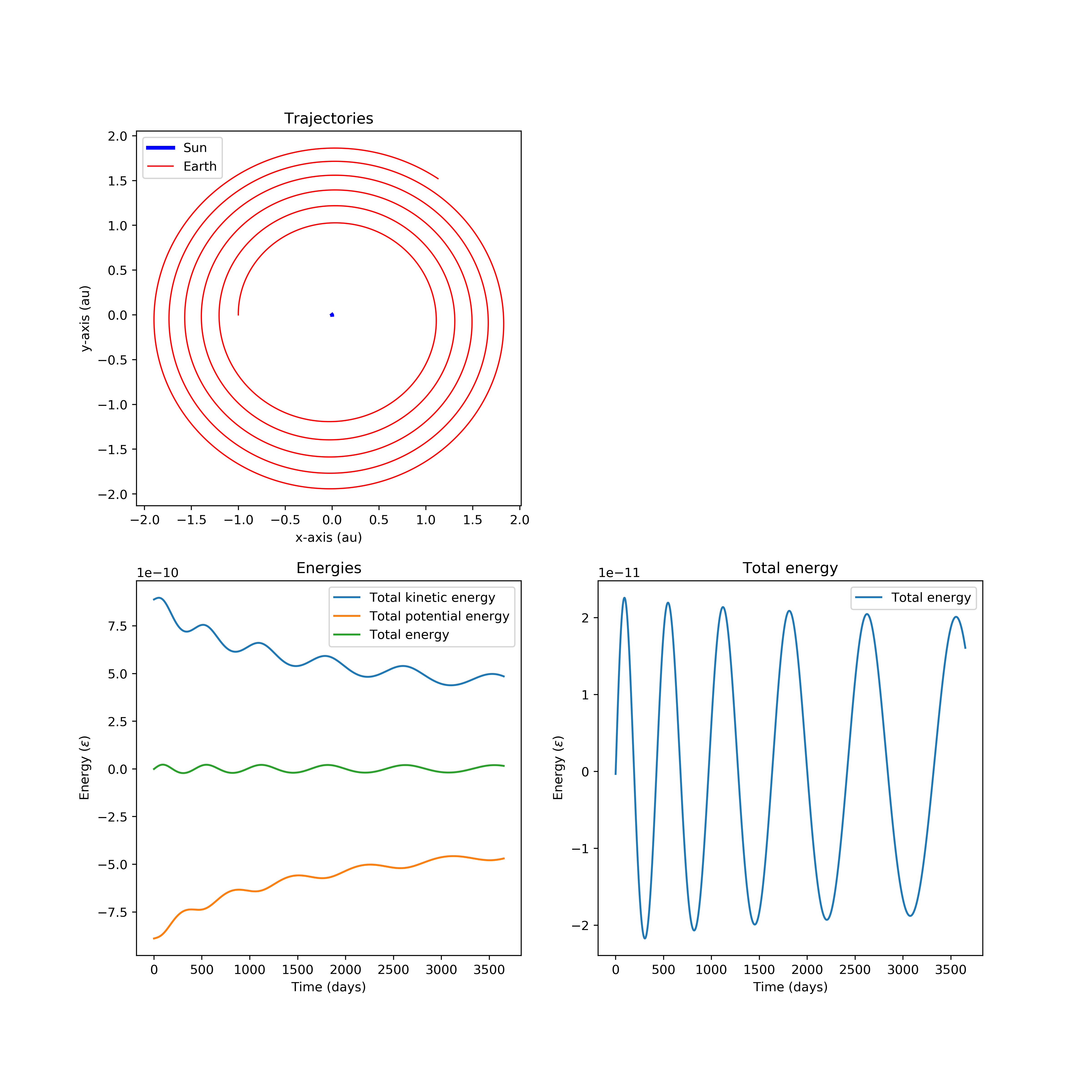As we know, this is not a very good representation of reality. Moreover, we see that something is off in the total energy of the system: even though energy is supposed to be conserved, we see fluctuations in the total energy that are large on the scale of the individual energies in the system. This is a clear sign of something being wrong.

If we instead implement the velocity-Verlet algorithm (using the same timestep as in the Euler case!) we find a much more reassuring picture: 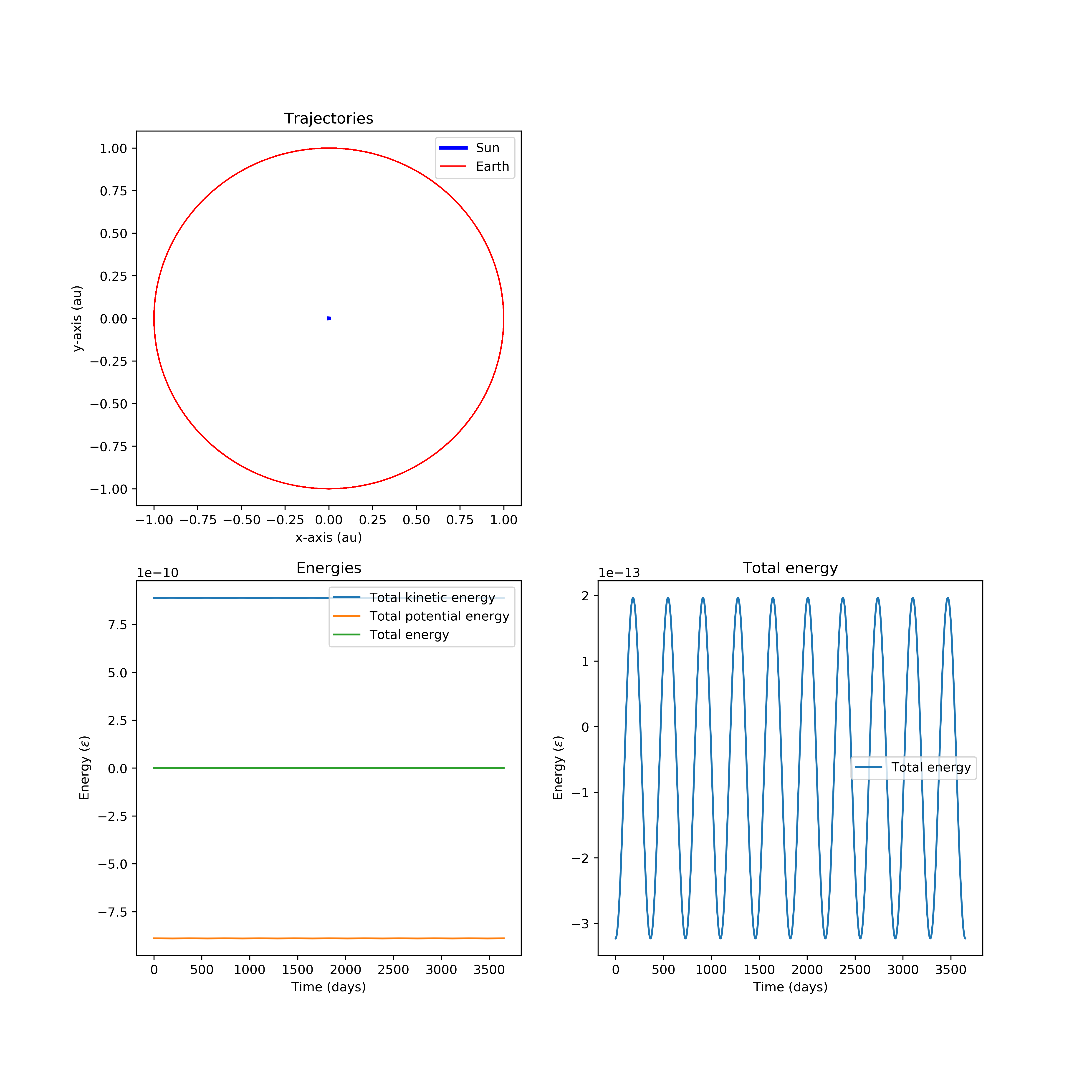Here the earth is in a stable orbit around the sun, and the fluctuations in the total energy of the system are now two orders of magnitude lower, much smaller than the individual energy contributions.

If you would like to further explore this example, the notebook that generates these figures can be downloaded here. Note that while in principle it will run for N bodies, this piece of code is not well suited for a molecular dynamics simulation! The usage of a class is debatable even when particles are not anonymous and identical, there are many nested loops, and various other parts of the code remain unoptimized. Try not to make these same mistakes!

Why are these algorithms actually better?

The difference to the Euler methods is actually very subtle, if you look for example at the velocity-Verlet algorithm. It turns out that these methods are part of a class of so-called symplectic integrators that are particularly suited for the time-evolution of Hamiltonian systems (which is the case for classical mechanics as we use here). If you want to learn more, we refer you to Jos' book or Wikipedia

Milestones

• Extend your code to more than 2 particles.
• Implement the velocity-Verlet algorithm.
• Investigate the conservation of energy in the system. Plot the evolution of the kinetic and potential energy, as well as their sum.
• Compare the results of energy conservation using the Euler and Verlet algorithms.
• Make an initial attempt to structure your code properly.

After week 3, you should have a code that simulates, for given initial positions and velocities, the classical motion of $N$ interacting particles with periodic boundary conditions. The simulation should conserve energy.