Week 2

Units

When you start coding the simulation of the motion of the Argon atoms, you soon find that the normal SI units (kg, m, s, etc) lead to numbers of quite different magnitude in the simulations: e.g. mass of the Argon atoms $\sim 6.6 \times 10^{-26}\,\text{kg}$ or distances of order Angstrom $\sim 10^{-10}\,\text{m}$.

Working with these different orders of magnitude is cumbersome, and prone to round-off errors. It is hence useful to identify some natural units in the simulation.

From the Lennard-Jones potential we can already find two natural units: $\sigma$ for position, and $\epsilon$ for the energy. Let us thus define $\tilde{\mathbf{x}} = \mathbf{x}/\sigma$ (and hence also $\tilde{r} = r/\sigma$). We can then define a dimensionless Lennard-Jones potential as

$$\tilde{U}(\tilde{r}) = U(r)/\epsilon = 4 ( \tilde{r}^{-12} - \tilde{r}^{-6})$$

So starting from Newton's second law for particle $i$:

$$m \frac{d^2\mathbf{x}_i}{dt^2} = \mathbf{F}(\mathbf{x}_i) = - \nabla U(\mathbf{x}_i)$$

We rewrite it in terms of the dimensionless position:

$$\frac{d^2 \tilde{\mathbf{x}}_i}{dt^2} = \sigma^{-1} \frac{d^2\mathbf{x}_i}{dt^2} = -\frac{1}{m \sigma} \nabla U(r_i) = -\frac{\epsilon}{m\sigma} \nabla \tilde{U}(\tilde{r}_i) = -\frac{\epsilon}{m\sigma^2} \tilde{\nabla} \tilde{U}(\tilde{r}_i)$$    

Note that from $\nabla U(r) = \frac{dU}{dr} \frac{\mathbf{x}}{r}$ we get $\nabla = \sigma^{-1} \tilde{\nabla}$. The only variable that still has a dimension is time $t$. If we also define a dimensionless time $\tilde{t} = t/(\frac{m\sigma^2}{\epsilon})^{1/2}$, the whole Newton equation becomes very simple:

$$\frac{d^2\tilde{x}_i}{d\tilde{t}^2} = - \tilde{\nabla} \tilde{U}(\tilde{r}_i)$$

In practice, one usually leaves away all the tildes over the units. Then, you just say: length is in units of $\sigma$, energy in units of $\epsilon$ and time in units of $(\frac{m\sigma^2}{\epsilon})^{1/2}$.

The advantages of this approach are:

• Less cumbersome numbers/constants/units to take care of in the program (less error prone)
• Simpler equations (easier to code)
• Insight into what are the expected length/time scales in our system

The last point is especially important. If $\sigma$ is a natural scale of length in our system, we expect a typical distance (such as inter-atom spacing) to be of order $\sigma$. If we put in the numbers for Argon to calculate our new unit of time, we arrive at $(\frac{m\sigma^2}{\epsilon})^{1/2} = 2.15\times 10^{-12}\,\text{s}$. So if we know what a typical distance and a typical time will be in our system, we can double check with the expected velocities.

From the equipartition theorem we have $v = \sqrt{3 k_B T/m}$. The natural unit of velocity in our units is $\sigma/(\frac{m\sigma^2}{\epsilon})^{1/2} = \sqrt{\epsilon/m}$. So, in dimensionless units

$$v/\sqrt{\epsilon/m} = \sqrt{3 k_B T/\epsilon} \sim \text{order unity}$$

Hence, the particle will move a typical distance of order $\sigma$ in time $(\frac{m\sigma^2}{\epsilon})^{1/2}$. For our dimensionless units, this thus means that the time step $h$ should be smaller than 1, and of order $10^{-2}-10^{-3}$. If your time step is too large, a particle can end up where it should not be. More specifically, extremely close to another atom, resulting in a huge repulsion for the next time step.

Some hints on the minimal image convention

We discussed earlier that our periodic boundary conditions also influence how the forces are calculated. In particular, we chose the convention that we will take only the force due to the nearest image of other particles. Note that this does not mean that an atom is only influenced by its nearest neighbouring atom. Instead, we just consider the closest of all 'image partners' (plus the original) of every atom for calculating interaction. The animation below highlights the image partners of the two red atoms that are closest to the green atom.

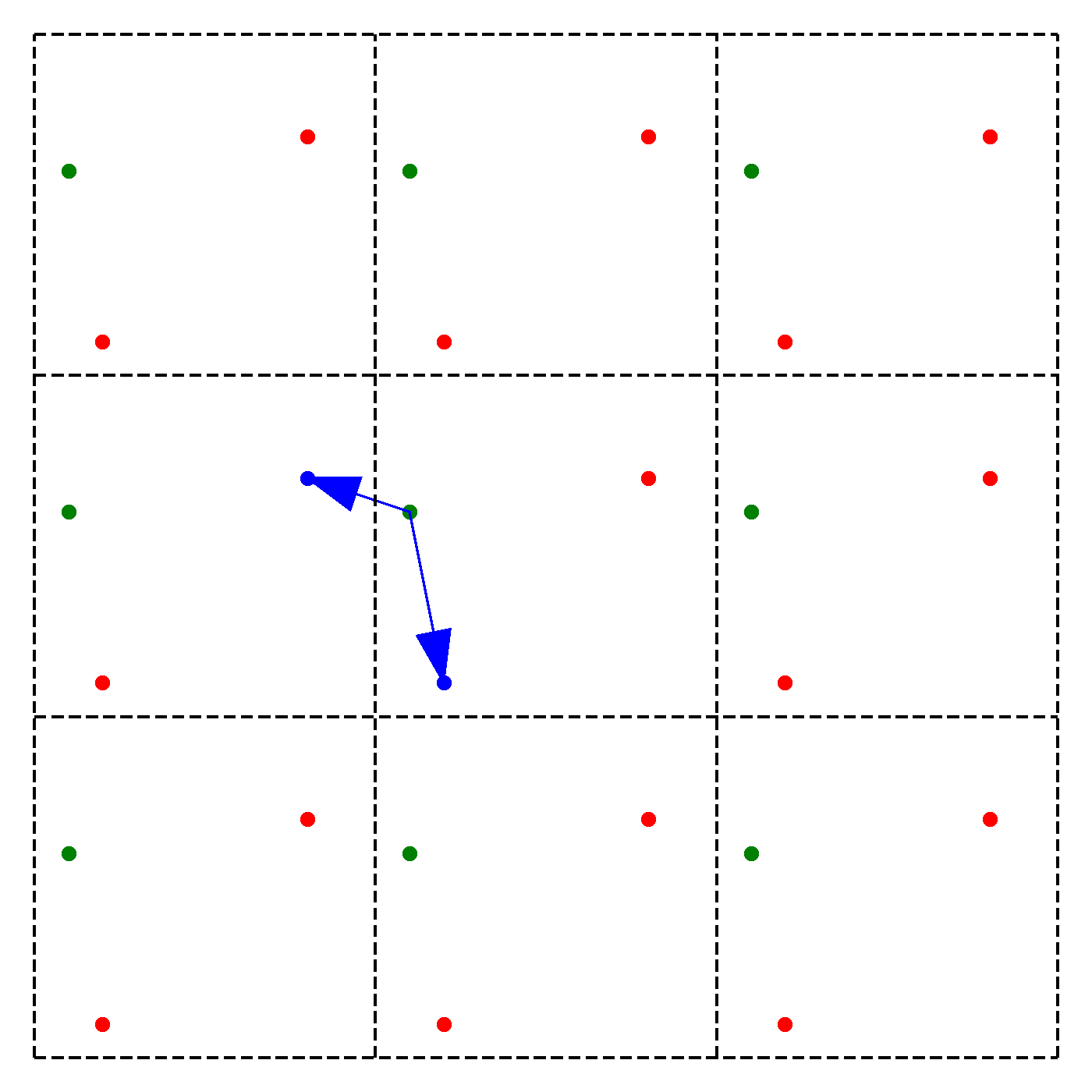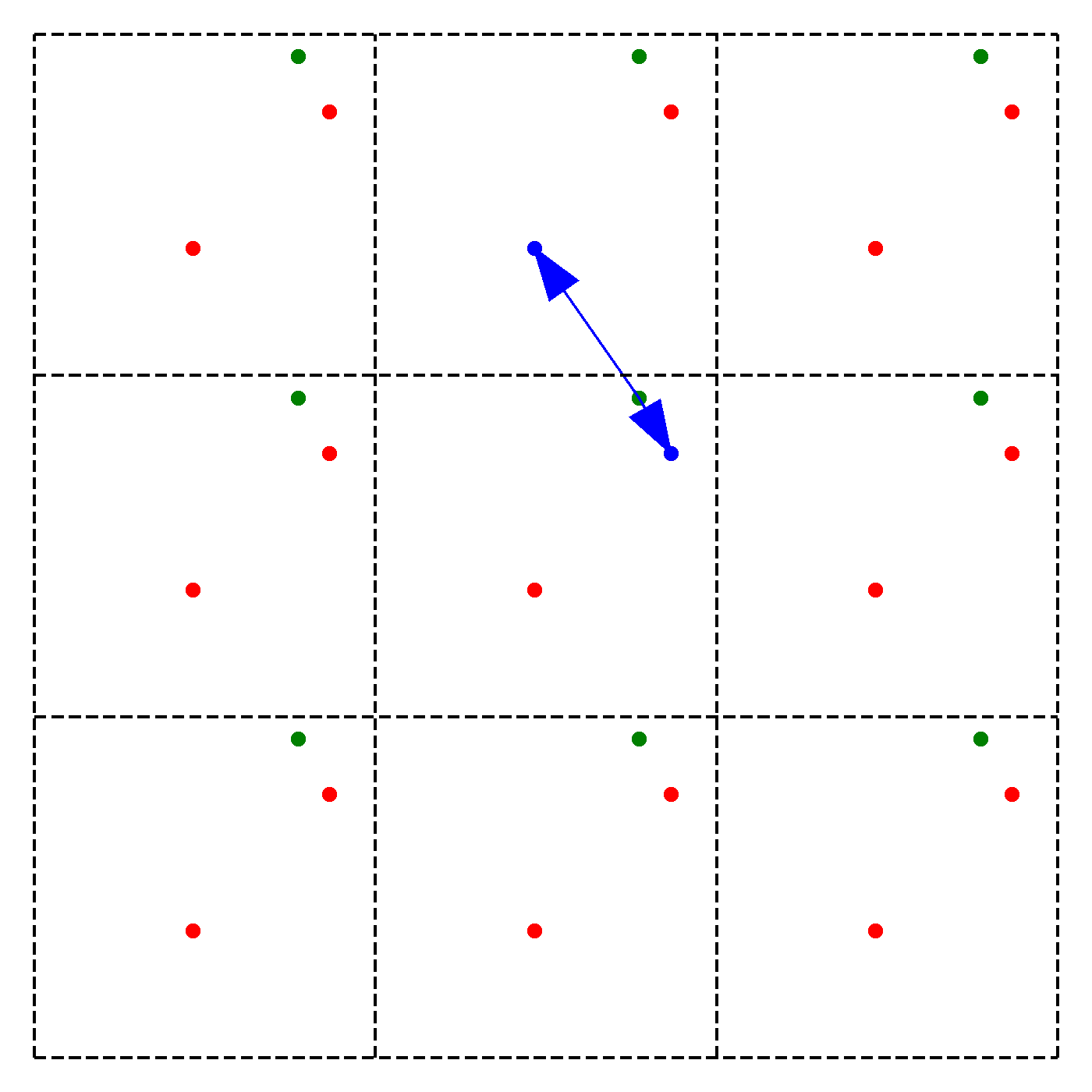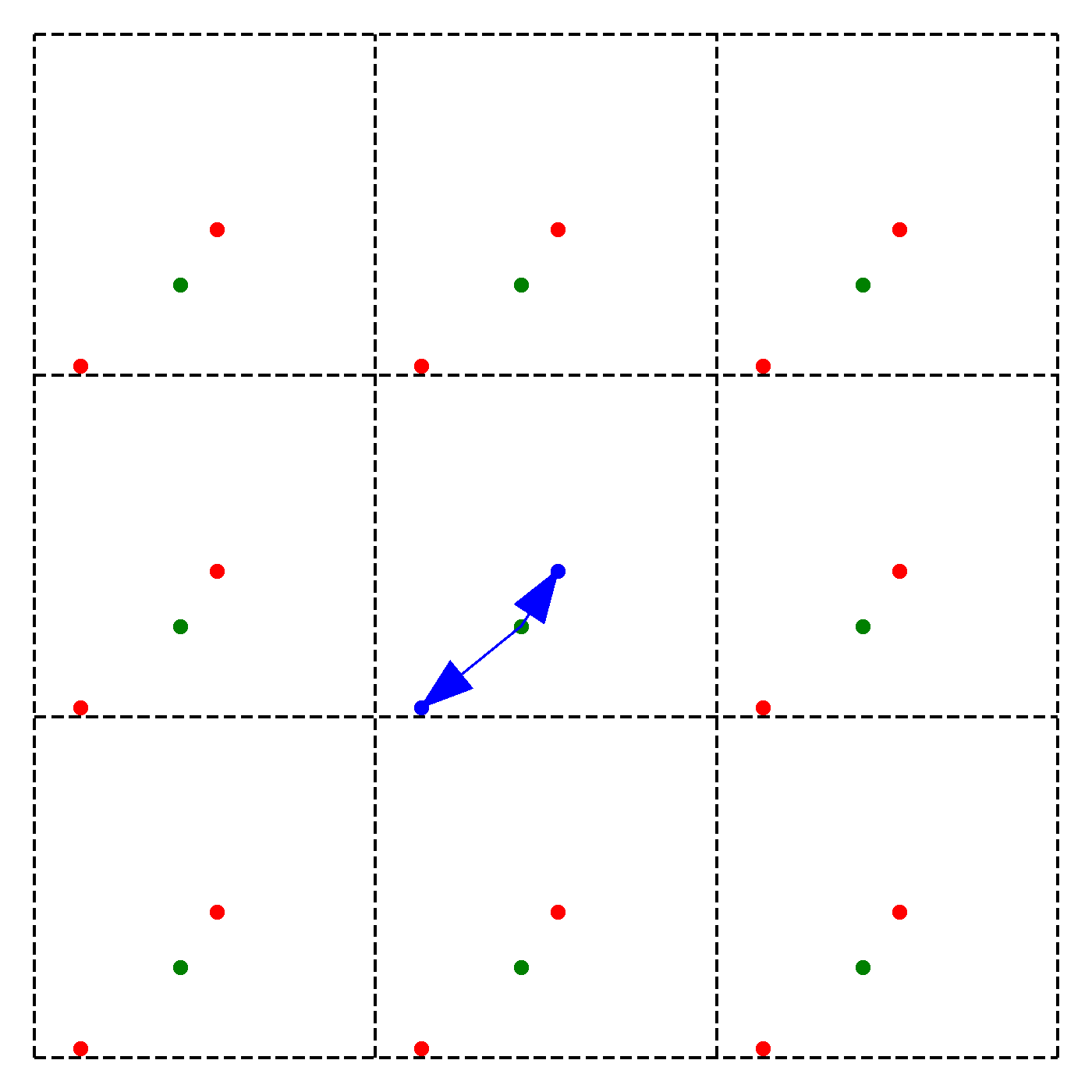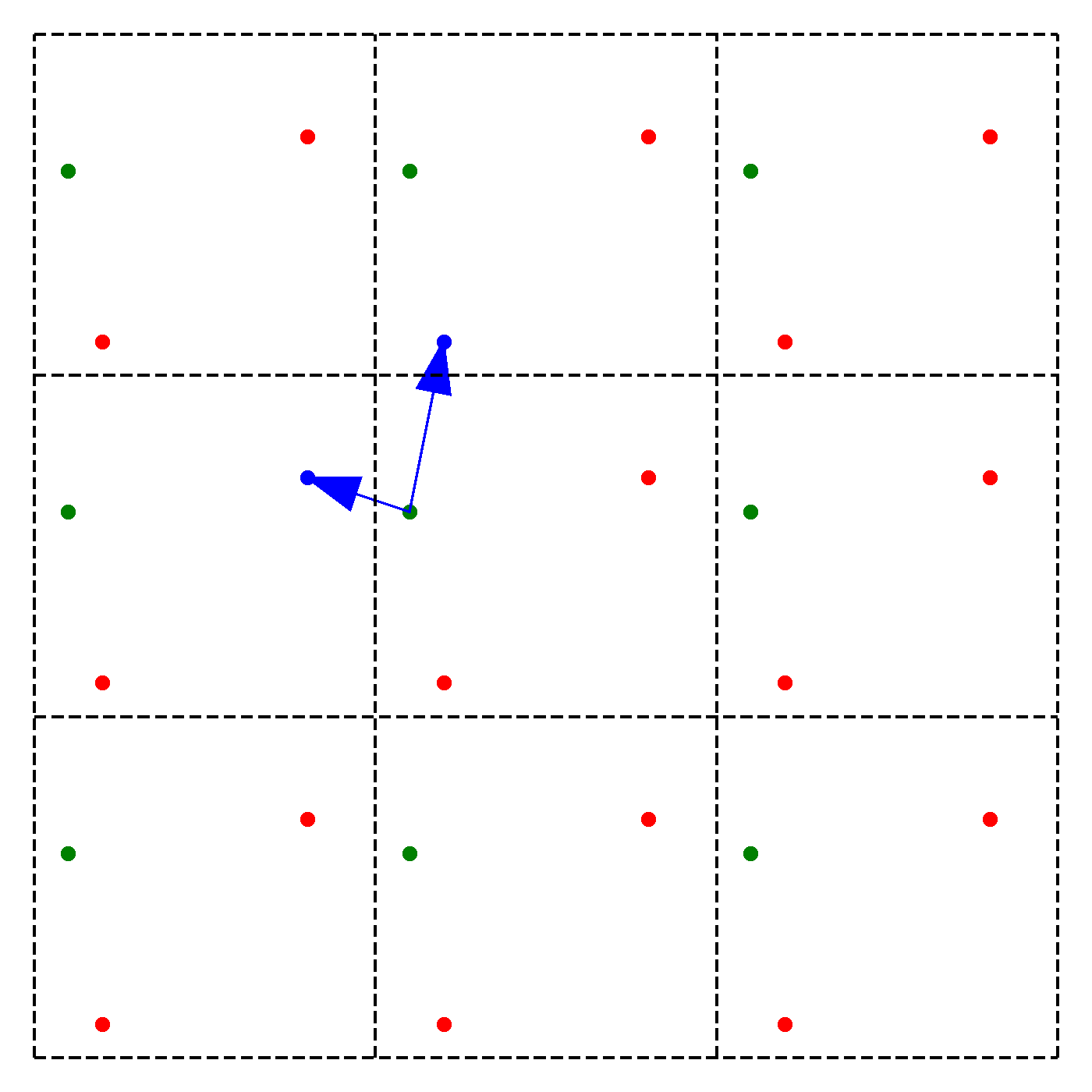
The blue arrows in the animation continuously point from the green atom to the closest mirror partners of the 2 red atoms. Naively, it would seem that thus to compute the force on particle $\mathbf{x}_i$ due to particle $\mathbf{x}_j$, we have to consider all the images of $j$ in 3D. This would give us 27 possibilities to check in total. To arrive at this number, extend the above animation to 3D and consider the amount of intern-atom distances to compute for the middle cell. However, since we are working with a orthogonal coordinate system, there is a significant simplification:

We need to minimize the distance $r_{ij}=\sqrt{(x_i-x'_j)^2+(y_i-y'_j)^2+(z_i-z'_j)^2}$ , where $x'_j, y'_j, z'_j$ are the coordinates of the original particle $j$ or an image, i.e. for example $x'_j = x_j$, $x_j+L$, or $x_j-L$,. However, since we can shift each of the coordinates individually, we can minimize $r_ij$ by minimizing each coordinate direction separately! Instead of 27 possibilities we thus just need to check 9.

The problem simplifies even more, since now we are effectively dealing with 3 seperate 1D problems. In particular we know that for a box of length $L$:

$$\begin{aligned} -L/2 < x_i - x_j < L/2 &\rightarrow x'_j = x_j\\ x_i - x_j > L/2 &\rightarrow x'_j = x_j + L\\ x_i-x_j < -L/2 &\rightarrow x'_j = x_j - L \end{aligned}$$

where $x'_j$ is now the closest image. Conditions like this are easily evaluated with numpy arrays. Another, even more compact formulation of the same is to write:

(xi - xj + L/2) % L - L/2

If you want to use this formulation, contemplate on why this does work (and check if we made a mistake ;) ). Use the formula that you are comfortable with!

Milestones

• Derive the expression of the kinetic energy in dimensionless units
• Change your existing molecular dynamics simulation to now use dimensionless units
• Implement the minimal image convention
• Simulate 2 atoms in 3D space. Choose their initial positions close to the boundary. This way, you can clearly see if the periodic boundary conditions work. Plot their inter-atom distance over time. Furthermore, also plot the kinetic and potential energy, as well as their sum, over time.