Project 1: Molecular dynamics

Writing a molecular dynamics simulation is of course a formidable task. During the lectures, we will guide you along the way towards writing a full-fledged simulation. At the end of the lecture notes of each week we list a set of milestones to aid you. These milestones also allow us to follow your progress, which helps in supporting you. These lecture notes flesh out a lot of the questions arising on the way to these milestones

Project goals

In this project we want to simulate phase transitions in materials: under which circumstances is the material a solid, a liquid or a gas?

In order to do this, we will simulate the classical motion of particles (for simplicity) in the material. The first choice is which material to simulate. Water, for example, is very complicated. It forms hydrogen bonds, the molecule is very asymmetric, etc. Considering we want something simpler, a noble gas is a very reasonable choice. Mainly because one doesn't have to worry about the formation of molecules. Historically, Argon (Ar) is the best studied and this is what we will do, too.

What is classical molecular dynamics simulation?

A molecular dynamics simulation aims to compute thermodynamic properties of a material (such as pressure or specific heat) by simulating the microscopic dynamics of an ensemble of atoms or molecules. Conceptually, this is based on the ergodic hypothesis that states that we can replace the ensemble average of statistical mechanics with a time average over the time-evolution of a specific ensemble.

The dynamics of the particles in the ensemble is approximated by classical mechanics: $N$ particles are moving according to the laws of Newton's mechanics, with each particle feeling a force generated by the $N-1$ other particles:

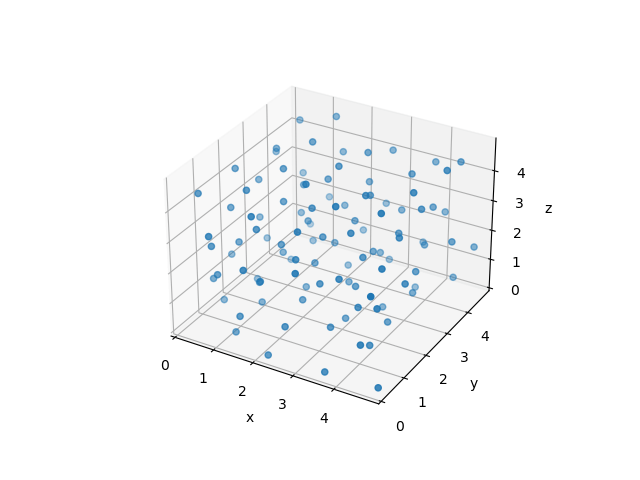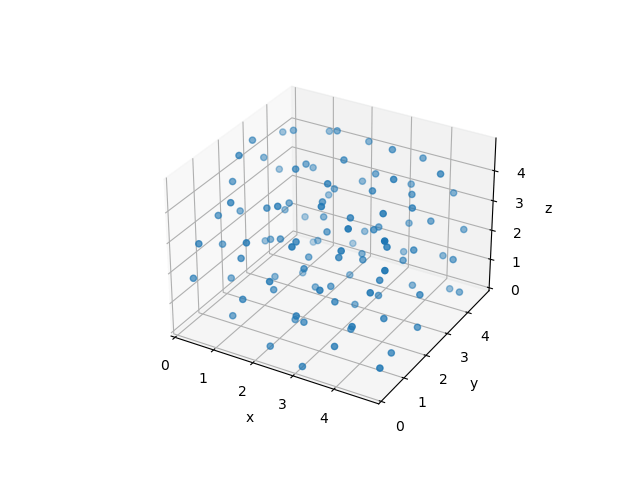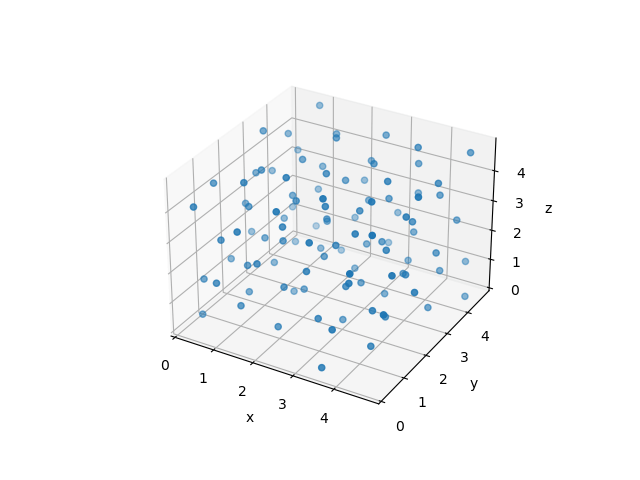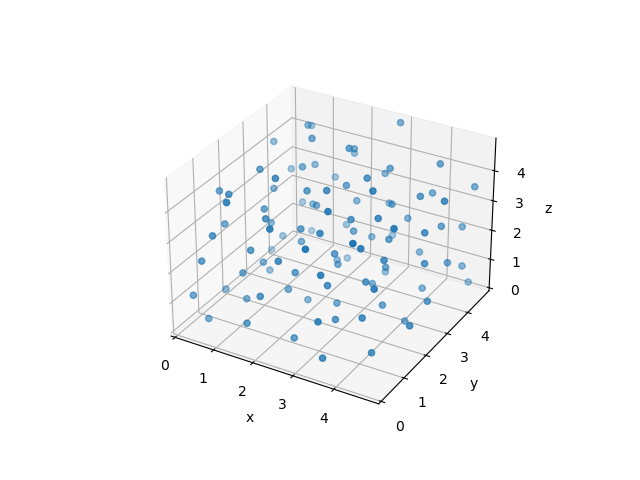
This is a complex $N$-body problem that can only be solved numerically.

The simulation of the $N$-body system yields not only nice-looking animations as above - even more importantly, it will allow us to extract thermodynamic properties! You will hear more about that in the later lectures.

For now, we will start by looking into the ingredients that go into the microscopic simulation:

• What equations govern the time-evolution? How do we solve them?
• What forces act between particles?
• We can only simulate a finite and small number of particles. How can we make sure we still obtain results applicable to a macroscopic solid?

Let us look into these aspects in more detail.

How do the particles evolve in time?

The motion of the particles is governed by Newton's equation. Hence, the particle $i$ will behave as follows:

$$m \frac{d^2\mathbf{x}_i}{dt^2} = \mathbf{F}(\mathbf{x}_i(t))$$

where $\mathbf{F}(\mathbf{x}_i(t))$ is the force acting on particle $i$ at time $t$. The force itself can be related to the potential energy due to the $N$ particles, $U(\mathbf{x}_1, \mathbf{x}_2, \dots, \mathbf{x}_N)$ as

$$\mathbf{F}(\mathbf{x}_i(t)) = -\nabla_i U(\mathbf{x}_1, \mathbf{x}_2, \dots, \mathbf{x}_N)\,,$$

where $\nabla_i$ is the gradient operator acting on coordinate $\mathbf{x}_i$. The force on particle $i$ thus depends on the coordinates of all particles!

These equations cannot be solved exactly, but need to be numerically solved approximately. Instead of continuous time, we thus will evolve the particles with finite time steps $h$.

A very simple way of doing this is to use the Euler method. If $\mathbf{x}_i(t_n)$ and $\mathbf{v}_i(t_n)$ are the position and velocity of particle $i$ at time $t_n$, the position and velocity at the next time $t_{n+1} = t_n + h$ are given by:

$$\begin{aligned} \mathbf{x}_i(t_{n+1}) & = \mathbf{x}_i(t_{n}) + \mathbf{v}_i(t_{n}) h \\ \mathbf{v}_i(t_{n + 1}) & = \mathbf{v}_i(t_{n}) + \frac{1}{m} \mathbf{F}(\mathbf{x}_i(t_{n})) h \end{aligned}$$

How do Argon atoms interact?

The form of the force entering the equations of motion is the only ingredient that can change the behavior of the ensemble. In fact, the choice of the force is what distinguishes different materials.

To get to an idea of the interaction between different Argon atoms, let us begin with the interaction between two. Argon atoms are neutral, so they do not interact via Coulomb interaction. However, small displacements between the nucleus and the electron cloud gives rise to a small dipole moment. Overall, the interaction between dipoles gives an attractive interaction that scales as $U(r) \propto 1/r^6$ where $r$ is the distance between two atoms.

On the other hand, Argon atoms do not come so close to each other that they overlap (they do not form molecules), hence there must be a repulsive force at small distances.

Both the attractive and repulsive interaction are parametrized in the Lennard-Jones potential, which takes the form:

$$U_\text{LJ}(r) = 4\epsilon \left(\left(\frac{\sigma}{r}\right)^{12} - \left(\frac{\sigma}{r}\right)^6 \right)$$

For Argon, the fitting parameters have been determined as $\epsilon/k_B=119.8\,\mathrm{K}$ and $\sigma = 3.405\,\text{Angstrom}$.

The total potential is then the sum over all pair-wise interactions:

$$U(\mathbf{x}_1, \mathbf{x}_2, \dots, \mathbf{x}_N) = \sum_{\alpha<\beta} U_\text{LJ}(|\mathbf{x}_\alpha - \mathbf{x}_\beta|) = \frac{1}{2} \sum_{\alpha\neq \beta} U_\text{LJ}(|\mathbf{x}_\alpha - \mathbf{x}_\beta|)$$

where the factor $1/2$ in the last expression is to avoid double-counting, and $|\mathbf{x}| = \sqrt{x^2+y^2+z^2}$ denotes the length of vector $\mathbf{x}=(x, y, z)$.

From this expression, we find the force then as

$$\mathbf{F}(\mathbf{x}_i) = - \nabla_i \frac{1}{2} \sum_{\alpha\neq \beta} U_\text{LJ}(|\mathbf{x}_\alpha - \mathbf{x}_\beta|) = - \nabla_i \sum\limits_{\substack{\beta \\ \beta\neq i}} U_\text{LJ}(|\mathbf{x}_i - \mathbf{x}_\beta|).$$

In the final expression, note that the sum is a single sum over $\beta$ (not a double-sum any more), as the derivative of all terms that don't involve coordinate $i$ are zero. Also, we used the fact $|\mathbf{x}_\beta - \mathbf{x}_i|=|\mathbf{x}_i - \mathbf{x}_\beta|$ and that each pair $i$, $\beta$ appears twice in the sum, canceling the factor $1/2$. Further simplifying, we arrive at

$$\mathbf{F}(\mathbf{x}_i)=\sum\limits_{\substack{\beta \\ \beta\neq i}} - \frac{dU_\text{LJ}}{dr} \nabla_i |\mathbf{x}_i -\mathbf{x}_\beta| = - \sum\limits_{\substack{\beta \\ \beta\neq i}} \frac{dU_\text{LJ}}{dr} \frac{\mathbf{x}_i - \mathbf{x}_\beta}{|\mathbf{x}_i -\mathbf{x}_\beta|}.$$

In which space do the Argon atoms sit?

We want to simulate an infinite system of Argon atoms - but obviously, a computer cannot simulate infinite space.

In practice, we will thus use a finite box of length $L$, with periodic boundary conditions (to emulate an infinite system). Recall that a periodic boundary condition for a wave function means: $\psi(x + L) = \psi(x)$, where $L$ is the size of the one-dimensional system. For a molecular dynamics simulation, we choose a periodic boundary condition to ensure that an atom will never reflect of a hard boundary. This has some subtle effects on the molecular dynamics simulation:

• If a particle leaves the box, it re-enters at the opposite side
• The evaluation of the interaction between two atoms is also influenced by the periodic boundary condition: the shortest distance between atoms may now include crossing the system boundary and re-entering. This is identical to introducing copies of the particles around the simulation box:

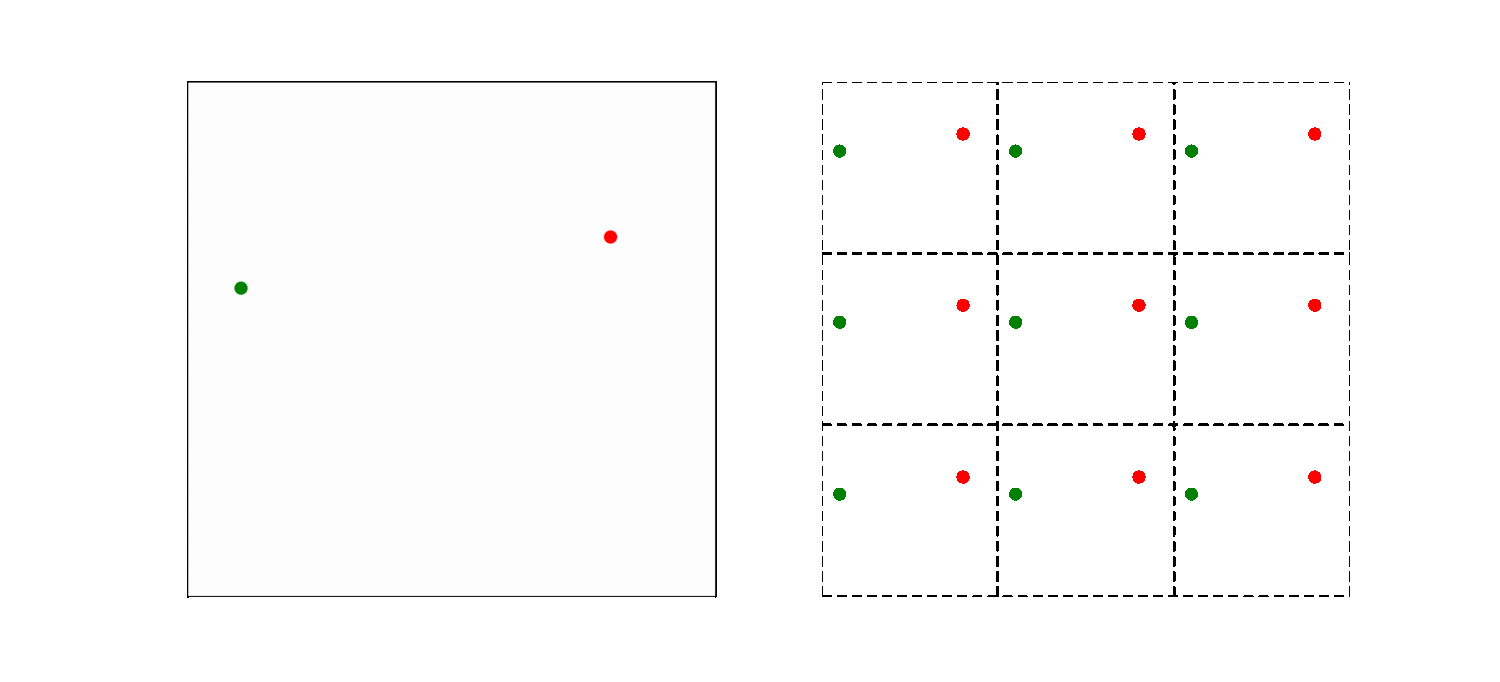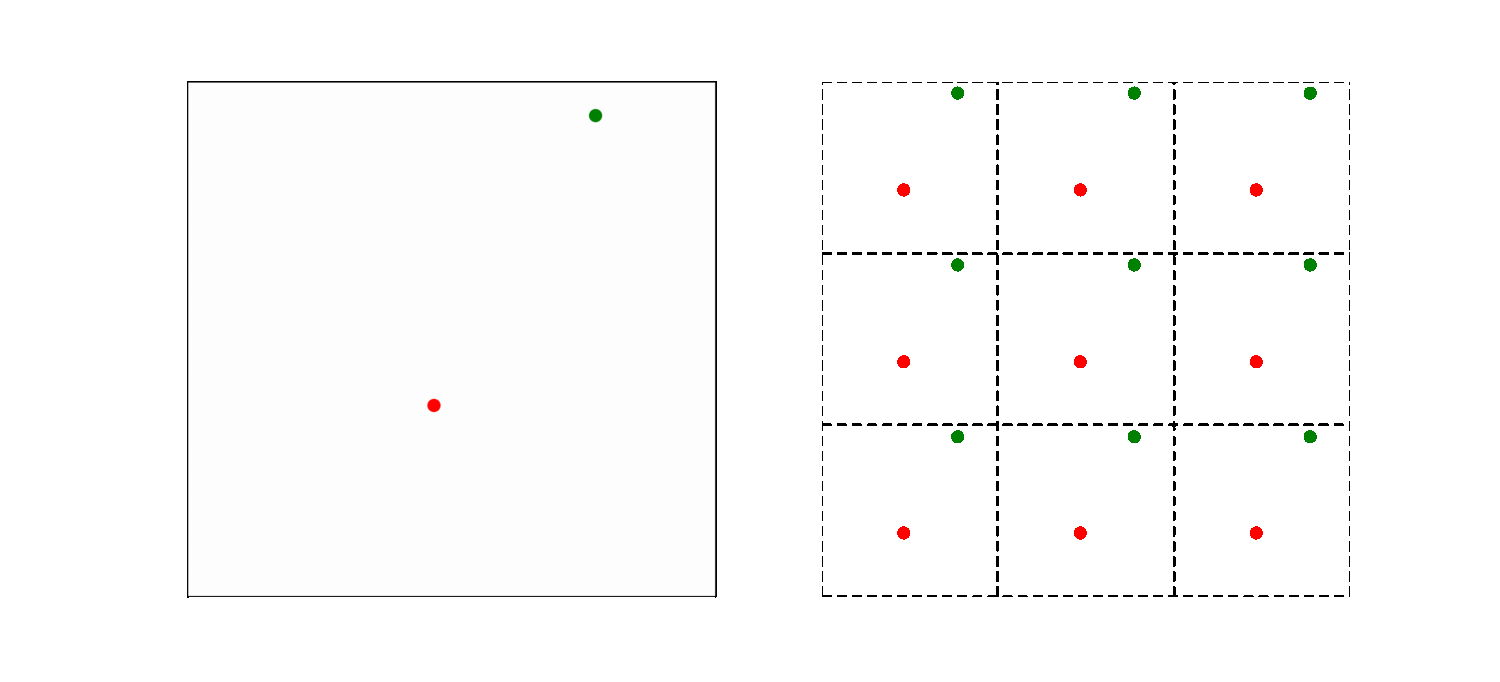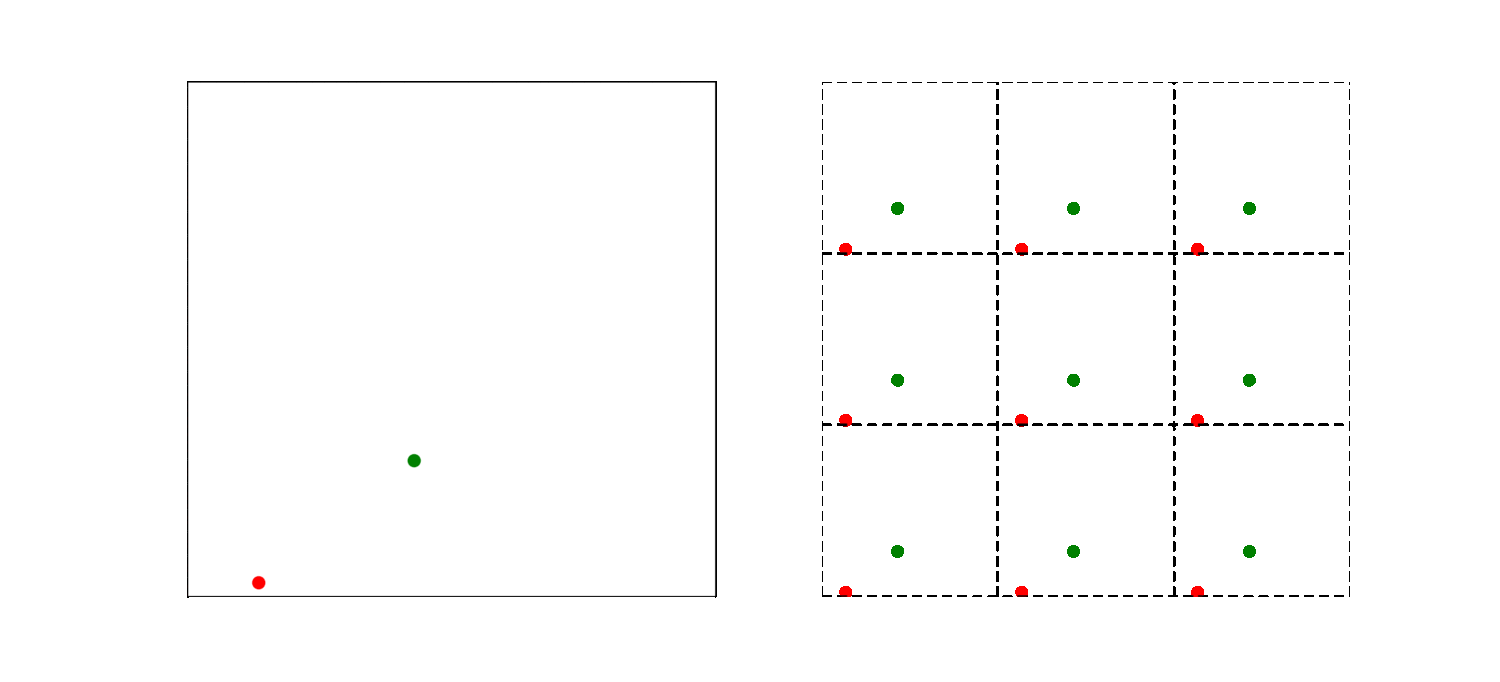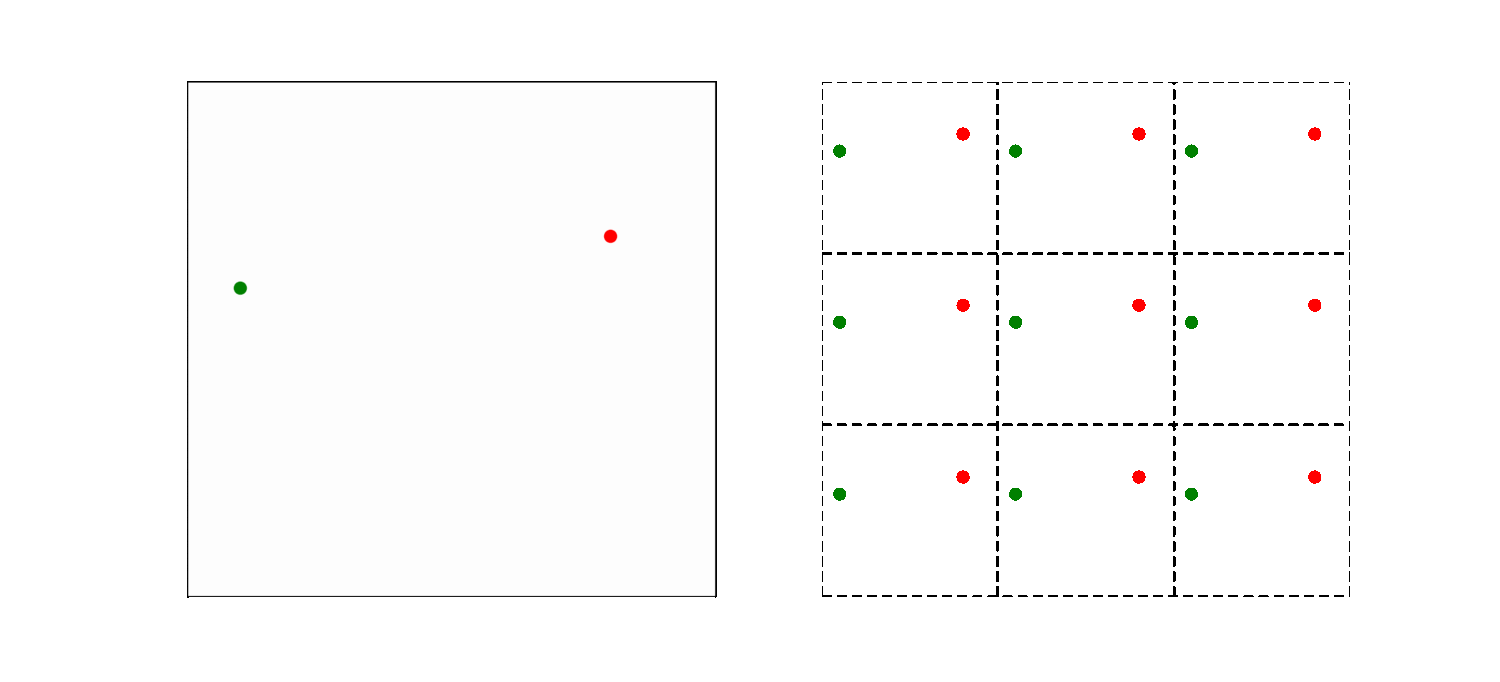The left part of the animation shows the actual simulation box, while the right part illustrates how the periodic boundary condition is implemented. The simulation box is now the middle square in the right part of the animation, the other 8 squares are copies. So a particle close to the far right system boundary is actually close to the left boundary too. As a result, the smallest distance between particles may thus not be the distance within the box! Here we use the convention to choose the pair of atoms that has the shortest distance. This is modeled by introducing copies of the particles in volumes bordering the actual system.

What to do

Play around with this system. Start by simulating the time evolution of a few particles in a periodic box, add the forces due to the Lennard-Jones potential.

It's easier to start with a 2D system, but plan to switch to 3D at a later stage.

Milestones

Here are a number of things you would need to achieve to satisfy the goals of this first week of the molecular dynamics project. At each milestone, think how you yourself would verify whether this is working or not. As stated above, start simple. Two dimensions and a small (2 is enough) number of atoms keeps your simulation orderly. This enables you to pinpoint errors more easily, as opposed to a three-dimensional simulation with 100 atoms.

Milestones

• Develop a way to store each particle's velocity and position at every timestep
• Calculate the force on each particle using the Lennard-Jones potential
• Implement the Euler method for time evolution
• Implement the periodic boundary condition
• Define a function that calculates the total energy of the system
• Make sure that you commit your code regularly to Gitlab.